Deviance analog to R^2

[jeffmoore]

hi all...

I've been using MARK for 3+ years, but this is my first post to this forum. Usually I just bother gwhite (sorry, Gary), so maybe this will take some pressure off him

So anyway, here's my question:

I understand the deviance of a candidate model, relative to deviance of a null model, may be interpreted as the proportion of deviance/variation in the data explained by a model.

Example:

Null deviance = 1000
Model deviance = 400
Proportion of variance explained by data = 1 - Dev(mod)/Dev(null) = 1 – 400/1000 = 0.60

This interpretation would be analagous to R^2 in linear regression


However, my best models in a current occupancy analysis I'm running explain 10 – 20% of the variation in my data, based on this above interpretation, even though I think my models are pretty good models.

To check this, I simulated some data (525 rows...5 occasions...3 groups), and then ran it through MARK. I fit a null model and the true model, which simply includes a group effect on psi (this is an occupancy model). Indeed, when I fit the ‘correct’ model to the data, the parameter estimates are very accurate. And yet, null deviance is 1286, and model deviance is 1177, so proportion of deviance explained by this model is only 1 – 1177/1286 = 0.08. Such a low “R^2” doesn’t make sense, given that the data literally came from this true model (since I simulated it), and given that the parameter estimates are close to correct. I would think this “R^2” analog should be close to 1 in this situation.

Any thoughts? I’d like to be able to estimate some measure of how much variation in data my models are explaining, but clearly the approach I’ve been assuming so far isn’t telling the correct story.

thanks very much,
jeff

[cooch]

Quick suggestion - try an analysis of deviance (ANODEV) on your simulated data. Although not widely used, the ANODEV provides a means of evaluating the impact of a covariate by comparing the amount of deviance explained by the covariate against the amount of deviance not explained by this covariate.


Check the MARK helpfile.

[darryl]

Jeff,
What is the log-likelihood value for the saturated model? 0.0? Maybe something there could be screwing you up? I'm not sure exactly what Gary considers to be the saturated model in the occupancy models...

Looking at the change in deviance values certainly indicates that the covariate is important

Darryl

[jeffmoore]

Evan and Darryl,

thanks very much for your suggestions, but...

I've considered ANODEV, but if I'm not mistaken, this only describes the proportion of deviance explained by different covariates relative to each other, or relative to a full model. It doesn't measure how much of the total (null) deviance is explained by the best model itself.

I think log-likelihood for the saturated model is 0, because the MARK help says this is so for any model with individual covariates.

Certainly I've been noting the change in deviance for the addition of a covariate, and so it's not hard to determine which covariates are yielding the most substantial improvement, but still, when null deviance is 1000, and adding an "important" covariate reduces deviance to 920, that's still only 8% of the total deviance explained.

Am I being pessimistic, or this sort of result typical?

thanks again,
jeff

[bmiranda]

I am seeking advice on a similar topic as Jeff posted in 2004, so I thought I would try to revive this thread and see if anyone has any current recommendations.

As with Jeff, I am looking for a way to calculate the equivalent of an R^2 value for my fitted models. Is the method that Jeff outlined using the deviance a good way to do it? I am aware of the Bootstrap GOF test, which seems like it might give me what I'm looking for, but it does not work with individual covariates (which I have). Is there a GOF test out there that does work with individual covariates?

Alternatively, if there is no adequate evaluation I can do using the data used to fit the model, I could do an evaluation using a validation data set. I have used only a subset of my data for model fitting and model selection, reserving another subset for validation purposes. I can calculate a predicted survival probability for each individual in my validation data set based on the fitted model, and I know how long that individual actually survived. But I am now struggling with how to quantify the relationship between observed and predicted due to the difference in units (probability of survival vs. years of survival). Does anyone know a good way to do this kind of validation? By the way, I am only looking at survival probability (Phi) and have a fixed capture probability (p = 1).

If anyone has any advice on how to properly do this kind of evaluation (predicted probabilty compared to actual data), or any pointers to relevant literature I would be very greatful for your assistance.

Thanks in advance for any advice!

Cheers,
-Brian

[cooch]

I am seeking advice on a similar topic as Jeff posted in 2004, so I thought I would try to revive this thread and see if anyone has any current recommendations.

As with Jeff, I am looking for a way to calculate the equivalent of an R^2 value for my fitted models. Is the method that Jeff outlined using the deviance a good way to do it? I am aware of the Bootstrap GOF test, which seems like it might give me what I'm looking for, but it does not work with individual covariates (which I have). Is there a GOF test out there that does work with individual covariates?

Alternatively, if there is no adequate evaluation I can do using the data used to fit the model, I could do an evaluation using a validation data set. I have used only a subset of my data for model fitting and model selection, reserving another subset for validation purposes. I can calculate a predicted survival probability for each individual in my validation data set based on the fitted model, and I know how long that individual actually survived. But I am now struggling with how to quantify the relationship between observed and predicted due to the difference in units (probability of survival vs. years of survival). Does anyone know a good way to do this kind of validation? By the way, I am only looking at survival probability (Phi) and have a fixed capture probability (p = 1).

If anyone has any advice on how to properly do this kind of evaluation (predicted probabilty compared to actual data), or any pointers to relevant literature I would be very greatful for your assistance.

Thanks in advance for any advice!

Cheers,
-Brian

A deviance R-square has been proposed as



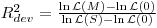
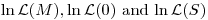where are the max likelihoods for the fitted (M), null (0) (i.e., intercept only), and saturated models (S).

The proposal is that deviance R-square compares the log likelihood gain achieved by the fitted model (in numerator) with the maximum 'potential' gain (the denominator). Since it is a measure of two log likelihood gains, this deviance R-square can be treated as an indicator of goodness-of-fit, and proportionate reduction in recoverable information, given the data.

Note that deviance R-square (as written) is of limited utility as a model selection tool, but might be OK for generating some measure of 'fit', which seems to be what you're after.

The *problem* is that the saturated model is not always specified, meaning you can't calculate the first term in the denominator. Which means for those models, you might be out of luck.

[bmiranda]

The proposed approach sounds simple enough, but as you point out:

The *problem* is that the saturated model is not always specified

So, do you have any advice on how to define a saturated model that includes individual covariates? I think I understand what defines a saturated model in the absence of individual covariates (all interactions), but it's not clear to me how to specify the saturated model when I do want to include the individual covariates. Would you simply construct the saturated model based on groups, and then add on the individual covariates? If you have any recommendations on building saturated models I would be very happy to hear them.

Thanks!
-Brian

[cooch]

The proposed approach sounds simple enough, but as you point out:

The *problem* is that the saturated model is not always specified

So, do you have any advice on how to define a saturated model that includes individual covariates?

No such thing. Related (conceptually) to the same reason there is no GOF test for a model with individual covariates.

I think I understand what defines a saturated model in the absence of individual covariates (all interactions), but it's not clear to me how to specify the saturated model when I do want to include the individual covariates.

As above, you don't. Your saturated model is the model without covariates -- the idea being that covariates can only improve model fit.

Would you simply construct the saturated model based on groups, and then add on the individual covariates? If you have any recommendations on building saturated models I would be very happy to hear them.

Thanks!
-Brian

It isn't that simple -- saturated models are a theoretical construct for a given model structure. For some data types, it isn't even clear what the saturated model would look like. See the - sidebar - on p. 3 of chapter 5.