Parameter Identifiability

[JKWinter]

Hello everyone! I'm somewhat new to MARK but I have a question about parameter identifiability and choosing which models to use in regards to identifiable parameters.

So here is the situation I am having: I have a time dependent model (for survival and recapture) that has the lowest AICc value, obviously that is the most parsimonious model and generally the model that best fits the data, but there are more than one parameters unidentifiable (either a 0.9999999 survival rate or a very high or 0 SE). I have a second model where recapture probability is constant where all parameters are identifiable, but the AICc value is higher. Which model would be best to use? Is the time dependent model still the better model to use because of the lower AICc value and I would just discuss that there is lack of data or the structure of the model is bad?

I have read the chapter 4 and Appendix F in the book about determining which parameters are identifiable but I am not finding any literature or anything in the book that talks about how to deal with these models and which ones are better to use.

[cooch]

I have read the chapter 4 and Appendix F in the book about determining which parameters are identifiable but I am not finding any literature or anything in the book that talks about how to deal with these models and which ones are better to use.

So, what did data cloning show you? If the parameters that aren't being estimated correctly are 'interior' parameters (meaning, not at the beginning or end of the time series), then the non-identifiability is 'extrinsic' (meaning, your data is insufficient to estimate those parameters). So, simply, you can't fit those models (being, fully time-dependent).

[JKWinter]

I think it might be more helpful to put the data here.

Parameter Estimate Standard Error Lower Upper
-------------------------- -------------- -------------- -------------- --------------
1:Phi 0.9999806 0.0058972 0.1203873E-253 1.0000000
2:Phi 0.3813039 0.0449027 0.2979501 0.4722893
3:Phi 0.2084220 0.0275661 0.1595003 0.2675721
4:Phi 0.4823504 0.1630207 0.2058206 0.7701306
5:Phi 0.2925366 0.0506085 0.2038533 0.4003975
6:Phi 0.4094875 0.1334621 0.1903284 0.6716613
7:Phi 0.9999907 0.0028254 0.2510457E-253 1.0000000
8:Phi 0.5626274 0.0479705 0.4674832 0.6533767
9:Phi 0.3546609 0.0349924 0.2894054 0.4258132
10:Phi 0.6604324 0.1490067 0.3459099 0.8773434
11:Phi 0.4632547 0.0550860 0.3585952 0.5712549
12:Phi 0.5914022 0.1370352 0.3226250 0.8147635
13:p 0.4013770 0.0603130 0.2907537 0.5230498
14:p 0.7313189 0.0696270 0.5761031 0.8449923
15:p 0.9999995 0.1672449E-03 0.2153186E-298 1.0000000
16:p 0.2994965 0.0699384 0.1819663 0.4510793
17:p 0.6344508 0.0629001 0.5049460 0.7470486
18:p 0.9999993 0.2622830E-03 0.1372892E-298 1.0000000

So I assumed that parameters 1, 7 and 15, 18 were unidentifiable because of their survival estimates and SE. I cloned the data (100 samples) and then it gave me SE ratios that were not close to 10. That's the bit that I took away from the data cloning appendix.

Parameters 1-6 and 7-12 are two separate attribute groups so it is the beginning parameters of each dataset.

So it seems that a fully time dependent model is not a good fit even though its AICc value is the lowest. And then that being the case, the best option is to use a model where all parameters are identifiable (ie constant data or others)? I hope I understand this concept enough but I very much appreciate the input.

[cooch]

The AICc is probably incorrect, since the number of parameters MARK is estimating is occasionally wrong (low) when you have a few extrinsically unidentiable parameters. What you should do is think about your model, figure out how many parameters should be identifiable, given the structure of the model,and then adjust the number of parameters accordingly. Doing so will undoubtedly change the AIC.

As to the other point, if at the end of the day your best model is simply fully time-dependent, then your analysis hasn't really told you much. At the other end of the spectrum, if your most parsimonious model is simply a 'dot' model, then your data probably aren't worth analyzing in the first place.

From the estimates you posted, my guess is you'll get some value in possibly adjusting the number of parameters. But, at the end of the day, its the models where you try to explain variation as a function of one or more temporally varying covariates you're interested in.

[JKWinter]

Ah yes fixing parameters I did not consider that. Mostly because I think I did not understand that concept very well. From what I read, fixing a parameter means I do not want it to be estimated from the data but rather I specify a parameter to a specific value (a value ranging from 0-1) and then it alters the survival/recapture estimates potentially? For example, regarding the data I posted in my previous message, I had four parameters that I deemed unidentifiable. Then when I fixed a value of 0.8 to parameter 1, it changed parameter 7 to a survival estimate of 0.91, making it an identifiable parameter with a SE Ratio of 9.999... with a lower AICc value. It still left Parameters 15 and 18 unidentifiable and Parameter 1 will have this fixed parameter but if I continue to change the fixed parameter values, then I would eventually end up with a point where I can say how many specifically are estimable and then go from there?

Thank you again for your input and I may have some more questions later because like I said I am new to MARK and some things I have read in the book and literature are unclear to me.

[cooch]

Ah yes fixing parameters I did not consider that. Mostly because I think I did not understand that concept very well. From what I read, fixing a parameter means I do not want it to be estimated from the data but rather I specify a parameter to a specific value (a value ranging from 0-1) and then it alters the survival/recapture estimates potentially?

I think you misunderstood -- I meant 'adjusting' the parameters that MARK reports, not 'fixing' parameters (although that can be an option if you're convinced a parameter really is 0, or 1).

Specifically, (i) select the model in question, where you think the number of parameters MARK reports is 'underestiamted' (which often happens with extrinsic non-identifiability), then (ii) ctrl-N, and adjust the the number of parameters up, to what it should be given the structure of the model.

[JKWinter]

Hi again. Thank you for all your input it has been a tremendous help. So far when I adjust parameters it does change the AIC. Follow-up question to that: if I were to change the parameters to lets say one less than what MARK estimated, does MARK know which one to not estimate? For example, if 13 parameters are estimated and I adjust to 12, does MARK know which one to adjust? I just notice that the NO of Parameters changes and the AIC but other than that I don't notice any differences.

Sorry for all the questions and I may have more but I'm trying to understand as much as I can.

[cooch]

Hi again. Thank you for all your input it has been a tremendous help. So far when I adjust parameters it does change the AIC.

As it must:

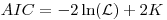
where K is the number of parameters.

Follow-up question to that: if I were to change the parameters to lets say one less than what MARK estimated, does MARK know which one to not estimate? For example, if 13 parameters are estimated and I adjust to 12, does MARK know which one to adjust? I just notice that the NO of Parameters changes and the AIC but other than that I don't notice any differences.

You're confusing a few things. First, you should never adjust *down*. MARK will not overestimate - only (potentially) underestimate the number of parameters. Second, manually adjusting the parameter count simply changes the AIC calculation, and nothing more.

Sorry for all the questions and I may have more but I'm trying to understand as much as I can.

No problem. I'd recommend a longer, more careful read of Chapter 4, where much of this is discussed.

[JKWinter]

So after a careful read of chapter 4, adjustment of parameters and AIC details are starting to make a lot of sense to me. So thank you for that recommendation.

I think my next (and maybe my last) question involves again the model selection when I am faced with models with nonidentifiable parameters which was part of my original post. I redid some MARK stats and got this: So I have three models where I have the same two attribute groups (habitat found in) on a four year encounter history. The two best out of those three models with the lowest AIC values were time dependent for survival and recapture, in both cases. The nonidentifiable parameters came from the phi and p values at the end of the time series so I have Phi1p2Phi2p3Beta4, a beta product in my capture history. However, the final time series (so the final parameters where there is the beta product) are the most critical part in my study, because those were the most recent captures which my study is focusing on much more. I have also adjusted the No. of parameters when I thought MARK incorrectly estimated the parameters and that increased the AIC.

My third model has time dependent survival but constant recapture, and according to the book, when survival or recapture are constant then ALL parameters become identifiable, regardless of time dependence. I wanted to choose that model because it correctly identifies all and the final parameters unlike my time dependent recaptures and before I mentioned the final time series is the most critical. So I am wondering if I can still choose that model to explain the survival of my captured animals or would it be better to use my time dependent models with a lower AIC value even though I have confounded estimates at my most important research section? Otherwise my option would be to use the constant model and just explain that there is not unidentifiability among the best fit models where potentially more captures are needed to accurately choose the time dependent models. Since most models have seen are chosen based on their lowest AIC value I thought this would be valid to ask before I go any further.

Again thank you for all the answers you have provided so far! I hope everything I described makes sense but in case it doesn't, this is my time dependent model with the lowest AIC below:

Real Function Parameters of {phi(h*t)p(h*t)}
95% Confidence Interval
Parameter Estimate Standard Error Lower Upper
-------------------------- -------------- -------------- -------------- --------------
1:Phi 0.9710146 0.1665993 0.3064271E-03 0.9999997
2:Phi 0.3613539 0.0522604 0.2663263 0.4686306
3:Phi 0.5469483 167.81930 0.6715572E-308 1.0000000
4:Phi 0.4597910 0.1239668 0.2424286 0.6936081
5:Phi 0.6534696 0.0721830 0.5023874 0.7788714
6:Phi 0.6115160 122.45062 0.8756268E-308 1.0000000
7:p 0.3731342 0.0867721 0.2234110 0.5518899
8:p 0.7014072 0.0871425 0.5096197 0.8415134
9:p 0.5466132 167.71641 0.6706497E-308 1.0000000
10:p 0.5612653 0.1680373 0.2513934 0.8297409
11:p 0.5753969 0.0722977 0.4314108 0.7076314
12:p 0.6113198 122.41142 0.8749042E-308 1.0000000

[cooch]

So after a careful read of chapter 4, adjustment of parameters and AIC details are starting to make a lot of sense to me. So thank you for that recommendation.

I think my next (and maybe my last) question involves again the model selection when I am faced with models with nonidentifiable parameters which was part of my original post. I redid some MARK stats and got this: So I have three models where I have the same two attribute groups (habitat found in) on a four year encounter history.

With a 4 year study, for a full time-dependent CJS model, you'll get only 4 separately identifiable parameters. The final survival and encounter paramters are confounded. Period.

The two best out of those three models with the lowest AIC values were time dependent for survival and recapture, in both cases. The nonidentifiable parameters came from the phi and p values at the end of the time series so I have Phi1p2Phi2p3Beta4, a beta product in my capture history. However, the final time series (so the final parameters where there is the beta product) are the most critical part in my study, because those were the most recent captures which my study is focusing on much more. I have also adjusted the No. of parameters when I thought MARK incorrectly estimated the parameters and that increased the AIC.

I'll be blunt. If your best model is full time-dependence, and you're interested primarily in the final estimates, you're out of luck. As noted above, they're confounded. Period. Unless you can constrain one of the two parameters to be a function of a covariate (say, constraining encounter probaability to be a function of effort, for example), you will not be able to pull them apart. Period.

Conceptually, fully-time dependent models in and of themselves are not interesting. Of course biological parameters must in reality vary over time (this isn't physics, where true temporal constants do exist). You toss a fully-time dependent model into the model set to represent one end of the spectrum, with 'dot' models at the other. If the 'dot' models get all the support, then your data are defficient in some fundamental way (i.e., give up, go do something else). If instead your best models are 'time-dependent', you've learned absolutely nothing except that they do better than 'dot' models. The question of time-dependence is a logical necessity, and not interesting in and of itself.The question you should focus in one is 'why is there time variation?', and focus on identifying plausible covariates.

My third model has time dependent survival but constant recapture, and according to the book, when survival or recapture are constant then ALL parameters become identifiable, regardless of time dependence.

Correct.

I wanted to choose that model because it correctly identifies all and the final parameters unlike my time dependent recaptures and before I mentioned the final time series is the most critical.

You don't choose the model - the data does. Look, if you simply want survival estimated over that final interval, then make that choice. Decide you're going to fix p, even if you have no reason to do it other than wanting an estimate of phi over the final interval, recognize that said estimate of phi might be strongly biased wrt to reality, and go from there. If this is your thesis (and it sounds like it is)), then your committee will wrestle with that.