I'm running RDPNE analysis with a small number of marked individuals (14), and while real estimates of U (number of Unmarked Individuals) seem reasonable,
derived estimates of N are much higher than expected (the difference between U and N is greater than the maximum number of marks in the population). This only
occurs when modelling alpha as a function of any individual covariates.
Nevertheless, estimates of
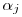 and
and 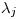 (intercept of resighting rate and mean resighting rate) also seem reasonable.
(intercept of resighting rate and mean resighting rate) also seem reasonable.Clearly there is something wrong going on on the deriving of
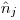 , the exact number of marked individuals on the population.
, the exact number of marked individuals on the population.The Good Book says it is derived as
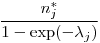 (18.4.1, p688), but my by-hand calculation doesn't match the results.
(18.4.1, p688), but my by-hand calculation doesn't match the results.When using individual covariates the deriving of
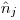 is done differently?
is done differently?Maybe the low number of individuals marked, and low number of individuals in some groups is able to bias
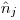 ?
?Any insight on this would be very appreciated!
Cheers,
Caio Kenup
***
Encounter histories and estimates below
- I kept only one individual covariate, but all the others (sex, age etc) present the same problem)
- U is modelled as 'U = ~ time' and all other parameters are constant
Encounter History:
- Code: Select all
ch captive
anathema 030102-00103050504070402080104030602060411070402040505030403 0
bjork ..............................+005-0-0-0-0-0-0-0-0-0-0-0-0-0 0
grey ..............................05030101-0-0-0-0-0-0-0-0-0-0-0 0
kanayeva ..................................................0902020106 0
lili ..........+00201-001-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0 0
lolita ..............................+0-0-0-0-0-0-0-0-0-0-0-0-0-0-0 0
luke ..............................04-0060605-0-0-0-0-0-0-0-0-0-0 0
luna ..........020203030402-0-00707020301010202050503040702080910 0
maia ..............................+0-0-002-0-0-0-0-0-0-0-0-0-0-0 0
malu ....................07110407060207020504-00101-0-00502010101 0
negra 0510060407050805-006050901-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0 1
sol ........................................+0-001-0-0-0-0-0-0-0 0
wallace ..............................010302-0020401-0-001.......... 1
x 0203050805060403-006060405080808050505-00906030305010202-005 1
Comparison of estimates
alpha= ~1 + time
alpha - real (last 5 intervals)
- Code: Select all
estimate se lcl ucl
5.3332387 1.0825030 3.5971441 7.9072271
2.5750835 0.7280453 1.4953436 4.4344692
3.1649404 0.8125586 1.9288759 5.1931012
3.4553933 1.0134059 1.9678061 6.0675403
4.9412111 1.0358542 3.2908123 7.4193132
alpha - beta (last 5 intervals)
- Code: Select all
estimate se lcl ucl
0.4817914 0.3833180 -0.2695118 1.2330947
-0.2462853 0.4310450 -1.0911336 0.5985630
-0.0400330 0.4143167 -0.8520938 0.7720278
0.0477690 0.4373981 -0.8095312 0.9050693
0.4054432 0.3868360 -0.3527553 1.1636417
Lambda (last 5 intervals)
- Code: Select all
estimate se lcl ucl
5.780045 1.0899755 4.0069378 8.337768
2.598571 0.7336351 1.5101127 4.471569
3.769199 0.8380829 2.4505262 5.797475
4.213964 1.0420259 2.6140737 6.793036
5.582182 1.0452474 3.8796027 8.031946
Unmarked Individuals
- Code: Select all
estimate se lcl ucl
17.5527260 3.7767529 11.5680380 26.6335730
29.8155940 9.1015770 16.6098120 53.5207520
24.5348360 6.0475842 15.2423900 39.4923740
20.5210930 5.5553673 12.1849990 34.5601410
17.4592410 3.7498138 11.5149520 26.4721120
N (last 5 intervals)
- Code: Select all
estimate se lcl ucl
22.582193 3.802787 16.271369 31.34066
35.243927 9.404081 21.078965 58.92767
29.769366 6.220069 19.852314 44.64039
24.661776 5.684443 15.789039 38.52060
22.501699 3.785882 16.218003 31.22002
alpha = ~1 + captive
alpha - real
- Code: Select all
estimate se lcl ucl
3.7645482 0.2194680 3.3583824 4.2198361
alpha - beta
- Code: Select all
estimate se lcl ucl
alpha:(Intercept) 1.2810913 0.0677920 1.1482191 1.4139635
alpha:captive 0.2078373 0.1016335 0.0086357 0.4070389
Lambda (last 5 intervals)
- Code: Select all
estimate se lcl ucl
4.293518 0.2059123 3.908529 4.716429
3.902010 0.2041100 3.522025 4.322990
4.489273 0.2068137 4.101876 4.913256
4.461688 0.2400205 4.015506 4.957447
4.489273 0.2068137 4.101876 4.913256
U (last 5 intervals)
- Code: Select all
estimate se lcl ucl
23.6103530 2.8586746 18.6386420 29.9082290
19.8254520 2.7494567 15.1263920 25.9842880
20.5773480 2.5664912 16.1298950 26.2510850
19.3622570 2.5249805 15.0113120 24.9743000
21.6910890 2.6451310 17.0947230 27.5233100
N (last 5 intervals)
- Code: Select all
estimate se lcl ucl
49.448587 2.933112 44.025782 55.53934
45.663685 2.820848 40.461088 51.53525
46.415581 2.637441 41.527389 51.87916
35.958628 2.582978 31.241881 41.38749
47.529323 2.717223 42.494990 53.16007
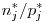 , where
, where![$p^*_j = 1/n^*_j \left[ \sum_{s=1}^{n^*_j} \left(1-\int_{-\infty}^\infty \exp( - \exp ( \sigma_{sj} z_{sj} + \alpha_{sj} ) ) \phi(z_{sj})dz_{sj} \right)\right]$ $p^*_j = 1/n^*_j \left[ \sum_{s=1}^{n^*_j} \left(1-\int_{-\infty}^\infty \exp( - \exp ( \sigma_{sj} z_{sj} + \alpha_{sj} ) ) \phi(z_{sj})dz_{sj} \right)\right]$](/forum/latexrender/pictures/ac17cdfe120723e01362296d5286cae0.gif)
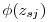 is the standard normal density. In terms of the betas reported by MARK,
is the standard normal density. In terms of the betas reported by MARK, 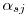 above is on the same log scale, but I believe MARK reports
above is on the same log scale, but I believe MARK reports 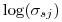 , so use
, so use 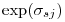 if calculating by hand from the betas.
if calculating by hand from the betas.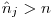 . MARK does not know the maximum number of marks that could be in the population, but is doing it's best to estimate
. MARK does not know the maximum number of marks that could be in the population, but is doing it's best to estimate 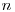 based on the encounter histories, and, in this case, the individual covariate on
based on the encounter histories, and, in this case, the individual covariate on 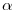 .
.