In other words, you don't know how to take a derivative of a function?

For the logit
If

then

If you look carefully, that is what is in the R code I posted, for each for the beta parameters in turn. You're using this derivative to form the gradient vector -- i.e., you're using the derivative of the logit transform.
For the sin, consult the table of transforms and back-transforms in the -sidebar- at the top of p. 22 in Chapter 6 of the MARK book. The back-transform on the sin link (again, assuming beta estimates from identity matrix) is
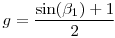
So, you simply differentiate
g with respect to

(as was the case for the logistic, above).

The rest is up to you.
Incidentally, if you have boundary estimates (which seems to be motivating your interest in using the sin link), then the MCMC approach might actually be more robust here.


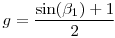
 (as was the case for the logistic, above).
(as was the case for the logistic, above).