Delta method for a ratio

[Dbradke]

I would like to calculate the variance for a ratio. The ratio is Ne/Nc (i.e., genetic effective population size/census population size). I estimated Ne using a genetics software (NeEstimator) and I estimated “Nc” (i.e., abundance) using Program MARK. I believe the best way to approximate a variance for this ratio is using the Delta method. However, I do not believe that these parameters are independent, which means I need the covariance (in addition to each estimate’s variance) to approximate a variance for the ratio. Because these estimates are not generated using the same software, I do not have a variance-covariance matrix. Does anyone have any suggestions for obtaining a covariance for two parameters estimated using different software programs or any other suggestions for obtaining a variance for this ratio? Any suggestions would be greatly appreciated! Thank you!

[simone77]

I am not sure I can give a useful answer here but in the worst case I hope, at least, to stimulate other, better-qualified, opinions.

The delta method is not that difficult to apply in order to estimate the variance of the derived parameter being a ratio of two estimates like in your case,

Nr = (Ne / N)

You may find quite a few resources to do it (e.g. the Ben Bolker's function "deltamethod" {emdbook} in R).

For me what makes your question of interest is what to do when, for any reason, you do not dispose of the covariance matrix. Maybe that, in your case, you might assume your samples (used for Ne and for Nc) are independent. In that case, you should be able to just set the covariance to zero and go on with the delta method (for instance I think you may do it using the deltamethod function in R).
Does it make sense to think your samples are independent?

[Rotella]

You might find Larkin Powell's 2007 paper in the Condor useful - [url]https://doi.org/10.1650/0010-5422(2007)109[949:AVODPU]2.0.CO;2[/url]

[Dbradke]

Thank you both very much for your replies. I agree that it is not too difficult to approximate the variance for a ratio using the delta method, especially following the Powell (2007) paper (which was actually the main reference I was using – it’s a great source!). The issue is that I don’t think Ne and N are independent, so I think it may be misleading to use a covariance of zero. However, it seems like that might be the only option, aside from not reporting a variance at all. Thanks again!

[cooch]

Thank you both very much for your replies. I agree that it is not too difficult to approximate the variance for a ratio using the delta method, especially following the Powell (2007) paper (which was actually the main reference I was using – it’s a great source!). The issue is that I don’t think Ne and N are independent, so I think it may be misleading to use a covariance of zero. However, it seems like that might be the only option, aside from not reporting a variance at all. Thanks again!

So, your 'thought problem' would be, if you assume independence, what does that do to your estimate of the variance? [Not hard with a bit of thought...]

Larkin's paper is indeed very good -- a very convenient tabulation of some common transformations, some interesting worked out applications, and a fair treatment of the underlying machinery [for the full treatment, Appendix 2 in the MARK book -- definitely less accessible than Larkin's paper, but partly because is has a different intent. Appendix 2 spends a lot of time trying to explain 'how it works', not just 'what to do'. Knowing how the Delta method -- or anything else -- works is important for those situations that arise when the Delta method doesn't work well.].

The other small comment about Larkin's paper is that there are a few nasty little typos in some of the equations which can cause problems (not at all Larkin's fault -- there are lot of clues in the paper that suggest said typos emerged when the editorial types -- who don't use LaTeX much, it would seem -- tried to typeset the equations...).

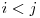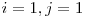For example, eq. 2 in the paper is not correct -- the double-summation in the second term should be of , not (following Seber, 1982). In the incorrect version, 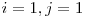is the variance, not the covariance. The equation requires 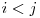to restrict it to covariances. And so on...

[Dbradke]

So, your 'thought problem' would be, if you assume independence, what does that do to your estimate of the variance? [Not hard with a bit of thought...]

Larkin's paper is indeed very good -- a very convenient tabulation of some common transformations, some interesting worked out applications, and a fair treatment of the underlying machinery [for the full treatment, Appendix 2 in the MARK book -- definitely less accessible than Larkin's paper, but partly because is has a different intent. Appendix 2 spends a lot of time trying to explain 'how it works', not just 'what to do'. Knowing how the Delta method -- or anything else -- works is important for those situations that arise when the Delta method doesn't work well.].

The other small comment about Larkin's paper is that there are a few nasty little typos in some of the equations which can cause problems (not at all Larkin's fault -- there are lot of clues in the paper that suggest said typos emerged when the editorial types -- who don't use LaTeX much, it would seem -- tried to typeset the equations...).

For example, eq. 2 in the paper is not correct -- the double-summation in the second term should be of , not (following Seber, 1982). In the incorrect version, is the variance, not the covariance. The equation requires to restrict it to covariances. And so on...

Thank you for the helpful response. If I followed Larkin's paper correctly, assuming independence should overestimate the variance (unless the two variables are actually independent), which I suppose would be the most conservative approach to take. I did also read through the appendix in the MARK Book on the Delta method, but it was a lot to wrap my brain around. I agree that the 'how it works' is very important though and will keep trying to understand that section better.