Dear all,
After simulations of capture histories and their analysis in MARK, it occurred to me that the mean survival rate found from an unconstrained time-varying survival model (like CJS) using the variance components is the arithmetic mean of annual survival rates. Is it right? Using a constant survival model also seems to provide an estimate of the arithmetic mean. If so, I am concerned, as people typically plug this mean into population models for simulations, therefore overestimating the overall survival, i.e. the geometric mean. I see in the Mark book a lot of discussion on the estimation of variance, but not much on the mean. It does not seem trivial to me. For instance, the logit link does not even preserve the arithmetic mean. Am I missing something?
Cheers,
-Yvan
geometric and arithmetic means of survival rates
4 posts
• Page 1 of 1
Re: geometric and arithmetic means of survival rates
yvan wrote:Dear all,
After simulations of capture histories and their analysis in MARK, it occurred to me that the mean survival rate found from an unconstrained time-varying survival model (like CJS) using the variance components is the arithmetic mean of annual survival rates. Is it right? Using a constant survival model also seems to provide an estimate of the arithmetic mean. If so, I am concerned, as people typically plug this mean into population models for simulations, therefore overestimating the overall survival, i.e. the geometric mean. I see in the Mark book a lot of discussion on the estimation of variance, but not much on the mean. It does not seem trivial to me. For instance, the logit link does not even preserve the arithmetic mean. Am I missing something?
Cheers,
-Yvan
Geometric mean makes little sense -- simple numerical example demonstrates. Suppose survival varies between 2 discrete values: 0.8, and 0.4. True mean is 0.6. Geometric mean over many samples, or a long time series, will always underestimate the true arithmetic mean. Following R snippet demonstrates this:
- Code: Select all
mm=matrix(0,2,1000);
for (j in 1:1000) {
env=sample(c(0.4,0.8),50,replace=T);
gm=prod(env)**(1/50);
am=mean(env);
mm[1,j]=am;
mm[2,j]=gm;
}
cat("arithmetic mean: ",mean(mm[1,]),"\n");
cat("geometric mean: ",mean(mm[2,]),"\n");
I can provide a more formal mathematical proof if needed (basically, Cauchy's original proof).
So, I think the question of arithmetic versus geometric is moot (this is not the case for lambda, though, as discussed elsewhere in the forum). What is more problematic (IMO) is (i) estimattion of the process variance for survival (see Appendix D), and (ii) the actual shape of the distribution, which the methods of moments assumes is symmetrical around the mean -- which it might in fact not be.
Related, see section 6.14 in the linear models chapter (6) for discussion of estimation of the mean.
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: geometric and arithmetic means of survival rates
yvan wrote:Dear all,
A I am concerned, as people typically plug this mean into population models for simulations, therefore overestimating the overall survival, i.e. the geometric mean....Am I missing something?
Cheers,
-Yvan
Yes -- the GM is an appropriate value to use for survival over an interval (say, over a number of years), but a projection model is based (typically) on an *annual* time step, at which point, your best estimate is the arithmetic mean.
Suppose you have 2 years: survival could be either 0.4, or 0.8. Thus, possible product survivals (i.e., probability of going from time t to t+2) are 0.16, 0.32 (twice 0.4*0.8, and 0.8*0.4), and 0.64. GM for these combinations is 0.4, 0.5657, and 0.8. Overall expected GM is in fact 0.583, which is more or less what the script in my first reply will yield.
But, the actual expectation for product survival will be 0.36, which is the square of the arithmetic mean, not the GM.
- cooch
- Posts: 1665
- Joined: Thu May 15, 2003 4:11 pm
- Location: Cornell University
Re: geometric and arithmetic means of survival rates
Thank you Evan for your quick response.
I am aware of the AM-GM inequality, and I am not denying it. I was just going through a period of doubt, wondering about the value of expectation in multiplicative processes.
I was too focused on a time interval basis. If I have been monitoring one cohort over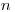 years and that I estimated perfectly the annual survival rates over the
years and that I estimated perfectly the annual survival rates over the 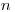 intervals, the number of survivors at the end of the study is
intervals, the number of survivors at the end of the study is 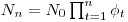 . I would expect the mean from MARK to be the geometric mean (
. I would expect the mean from MARK to be the geometric mean (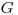 ) so that I can simulate the cohort and get to the same number of survivors using
) so that I can simulate the cohort and get to the same number of survivors using 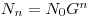 . However, in this case, using the arithmetic mean would lead to an overestimated number of survivors. But you're right, it does not really work like that in matrix population models.
. However, in this case, using the arithmetic mean would lead to an overestimated number of survivors. But you're right, it does not really work like that in matrix population models.
I am aware of the AM-GM inequality, and I am not denying it. I was just going through a period of doubt, wondering about the value of expectation in multiplicative processes.
I was too focused on a time interval basis. If I have been monitoring one cohort over
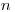 years and that I estimated perfectly the annual survival rates over the
years and that I estimated perfectly the annual survival rates over the 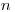 intervals, the number of survivors at the end of the study is
intervals, the number of survivors at the end of the study is 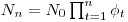 . I would expect the mean from MARK to be the geometric mean (
. I would expect the mean from MARK to be the geometric mean (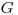 ) so that I can simulate the cohort and get to the same number of survivors using
) so that I can simulate the cohort and get to the same number of survivors using 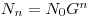 . However, in this case, using the arithmetic mean would lead to an overestimated number of survivors. But you're right, it does not really work like that in matrix population models.
. However, in this case, using the arithmetic mean would lead to an overestimated number of survivors. But you're right, it does not really work like that in matrix population models.- yvan
- Posts: 2
- Joined: Sun Dec 04, 2011 5:27 pm
4 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 1 guest